Data Representation

Binary Numbers

When computers interpret data they cannot read like we humans do; they cannot understand the human language. Instead, computers communicate and understand data in binary; a system that uses 1s and 0s to represent data. The 1’s and 0’s are created through electrical circuits turning on and off. ‘ON’ = 1 and 'OFF' = 0. Each digit or value represented as a 1 or 0 is called a “Bit” and 8 Bits is measured as 1 “Byte”. An example of this is the following string:

01001101 – The entirety of these digits is known as a byte and any single digit is called a bit.

Because a computer can only read binary it must use strings of binary to represent data that humans can understand and use. In the computer’s motherboard, characters are stored in the computer’s memory.
As an example… if I were to press ‘k’ on the keyboard… the computer would see that in binary. In this case the binary code for ‘k’ is ‘01101011’. This would go to the computer chip as this byte of data and then be interpreted as the number 107. The computer would find the letter represented by 107 (the letter k) and display it on the screen.

An example of a string of binary to make a sequence is:
Mark F = 01001101 01100001 01110010 01101011 00100000 01000110
(The black code represents the space)

We, as humans, use the base 10 counting system or denary meaning that there are ten different digits to count with (0,1,2,3,4,5,6,7,8,9). The computer however uses the base 2 system which means that it can only uses 2 digits and, therefore, requires a different method of counting. The base 2 system counts by starting with 1 and then each next digit is double the previous value. It also counts from right-left.
This string of binary – 00000001 – would count as 1 as the only digit which is classed as ON is the first digit (which represents 1).
This string of binary however – 00000010 – would be 2 as the next digit along has a doubled value than that of the previous bit which is 1.
This would mean that 00000100 would be 4 and so on and so forth.
Following this counting system, we can determine how many bits and bytes are required to represent all characters on a keyboard. An English keyboard has 127 different characters on it. This means that, if we follow the base 2 (binary) method of counting – 1+2+4+8+16+32+64 = 127. This means that to represent every character on that keyboard, you would need 7 bits to represent all the characters by number. This brings us to conclude that 1 byte is required as 7 bits would round up to 1 byte. This brings us to look at the ASCII table to which I will refer to later. The ASCII table is the reason why the denary number 107 represents ‘k’ on the keyboard.

Negative Binary Numbers

Negative numbers are vital in everyday practice such as representing a temperature below 0 or just a simple value below 0. There are 2 ways of counting negative numbers in binary. The first is the simple Sign bit system and the second and more complicated but useful way is Two's compliment.

The Sign bit system is the first way of representing negative numbers in binary. Because computers only use 1s and 0s you cannot represent a negative number in binary by just placing a sign in front of the binary number because signs such as positive and negative are characters which the computer cannot directly interpret.

The way that the Sign bit system creates a negative number however, is by adding one bit in front of the original number and using that bit to show a positive or negative value. The ‘0’ or ‘OFF’ value represents positive and ‘1’ or ‘ON’ value represents the number being negative.

For example:
Original number - 01000010 (66)
Sign bit variant – 11000010 (the 1 at the front means that the number is negative)

The problem with Sign bit is that the number 0 has 2 representations.
Original number - 00000000 (0)
Sign bit variant - 10000000 (also 0)

There is no such thing as '- 0' it is just 0 and yet 0 can have 2 different ways of being written due to Sign bits method of conversation. This is why Two's complement is better; because it fixes the representation of 0 from the Sign bit method.

Two’s compliment is the preferred way of representing negative numbers in binary. The Two’s complement method of representing a negative value is made in a computer by inverting the binary code of the original number and then adding a bit into the code.
Here is an example of how Two’s complement is found:

Original Number - 00011011 (27)
One’s Complement - 11100100 (The values have been inverted)
Add 1
Two’s Complement - 11100101

ASCII

The term ASCII stands for “American Standard Code for Information Interchange. It was originally used commercially in 1963 and used to be the main way of storing English characters in computers. Earlier, I referred the letter ‘k’ in a computer’s memory which was represented by the number 107. This is due to the ASCII table listing ‘k’ as its 107th character. The ASCII table lists 127 different characters from the average English keyboard and lists them, each character having a different value in binary. It is very easy to decode and understand due to it only having 127 characters but there is 1 huge disadvantage. It may contain all English characters… but what about all the thousands of characters in other languages that are not catered for? ASCII cannot cover them as it only uses 7 bits which can only count to 127. This is where Unicode comes in.

Unicode

The ASCII table is very limited as it only ever uses 7 bits out of 8 meaning that it is space inefficient as, with each character, there is 1 bit of data being wasted. When the World-Wide Web came along and files were being sent from country to country, because ASCII only represented English characters, other countries came up with alternative coding systems. This meant that, when documents were sent from country to country, they came out at the other end in a very confusing state as the computer could not understand the other coding system. With communication between countries becoming vital, a problem arose. This is a major issue as there are well over 100,000 different characters from various language throughout the world while the ASCII table can only account for characters 0-127. This is how Unicode came into being. Unicode can account for every character from every known language. The most popular and widely-used version of Unicode is UTF-8. We can see from this image that Notepad++ gives the option to use UTF-8. It is very popular and widely-used because it is very versatile. Although UTF-8 is used the most, there are other type of UTF. UTF-32 uses 4 bytes (32 bits) and, therefore, 33,554,432 characters can be produced. UTF-16 uses 2 or 4 bytes (16-32 bits), meaning that it can create either 65,536 or 33,554,432 characters.

UTF-8

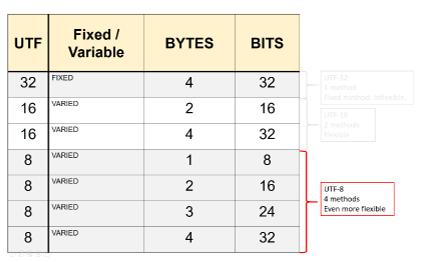UTF-8 is considered more versatile because it can use 1, 2, 3 or 4 bytes (8, 16, 24, 32 bits) 256 characters - 65,536 characters - 33,554,432 characters - 4,294, 967, 269 characters respectively. This means that it can operate on several different levels so that, depending on the amount of data, it can use the appropriate number of bytes to accommodate data in the most efficient manner. We can see this from the table to the right that, UTF 32 is fixed at requiring 4 bytes, UTF 16 has 2 variants and UTF 8 has 4 variants. The way that UTF-8 uses its bytes in the most efficient manner is simple. For the characters contained in the ASCII table (first 128 characters) UTF only uses 1 byte to represent them. Once it gets to characters out of the ASCII table (above 128 characters) then it will use 2 bytes which will accommodate the next 1920 which would include most Latin alphabets as well as languages like Greek and Arabic. Three bytes would be required to accommodate even more languages while 4 bytes is often used for pictorial and mathematical symbols. UTF-8 is extremely efficient as it only uses the bytes that it needs to at any one time which, therefore, makes it very space efficient I data use.

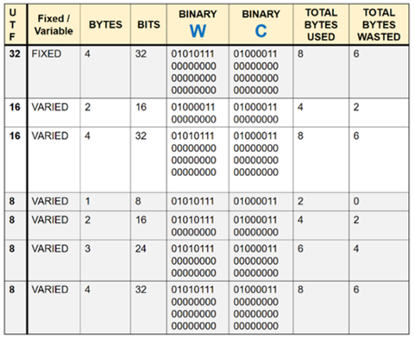This table explains this point clearly. I chose the letters ‘w’ and ‘c’ as example letters to refer to my college – Wairarapa College. From looking at the top row we can see that, when typing the simple letters ‘w’ and ‘c’, UTF-32 is not the best option as it would waste 3 bytes of data as only one byte is required to write each letter. That is 6 bytes wasted for 2 characters alone. Looking at row 2, we can see that UTF-16 also wastes bytes. This shows how UTF-8 is better; because, while the other methods waste bytes, UTF-8 is limited to 2 bytes and, therefore, uses the lowest amount of bytes needed with minimal waste. If UTF-32 were used in a text document containing 5000 characters of simple English (the average amount of characters on a single page), that is 15,000 bytes wasted in the entire document when only 5000 bytes are required.

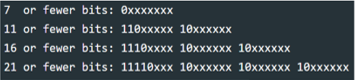The pattern on the left is used to accommodate a binary string of any character. Each byte starts with a sequence that shows how long a binary number is which tells the computer which variant of UTF-8 is being used. Encoding in UTF-8 is not as simple as placing digits into bytes and then using it. The computer requires extra information so that it knows which variant (1 byte, 2 bytes, 3 bytes and 4 bytes).

The table below explains this point clearly. I chose the letters ‘w’ and ‘c’ as example letters to refer to my college – Wairarapa College. From looking at the top row we can see that, when typing the simple letters ‘w’ and ‘c’, UTF-32 is not the best option as it would waste 3 bytes of data as only one byte is required to write each letter. That is 6 bytes wasted for 2 characters alone. Looking at row 2, we can see that UTF-16 also wastes bytes. This shows how UTF-8 is better; because, while the other methods waste bytes, UTF-8 is limited to 2 bytes and, therefore, uses the lowest amount of bytes needed with minimal waste. If UTF-32 were used in a text document containing 5000 characters of simple English (the average amount of characters on a single page), that is 15,000 bytes wasted in the entire document when only 5000 bytes are required.
The basics of encoding in UTF-8 are as follows:

  1. Determine how many digits the character requires.
  2. Replace the X’s in the left-most byte with the left-most digits of the binary character code. Remember to keep the digits in order.
  3. Once the left-most byte has been filled, move to the next byte and fill the X’s in that byte with the next number of digits from the binary code.
  4. Repeat this until all digits from the character code are in the new format.
  5. Once all digits have been integrated, any left-over X’s are to be filled with 0’s.

Another way to explain this method of encoding is to use an Asian character. Here is an unusual character randomly selected from an online Unicode chart – the Kanji character 用. The step we take to encode this in UTF-8 is to first find the binary for the character; in this case being ‘01110101 00101000’ (I found this code by inputting the character into a binary translator that I will show later in this section). Because it has 16 bits, we will use the 3-byte variant which accommodates for this. We take the last 4 digits and fill them in the spaces of the 4 X’s in the left-most byte. This would make the first byte ‘11100111’ as the bits from the character are kept in order and just placed in the first byte. The next byte would be ‘10010100’ as it uses the next number of bits from that charter and places them in the next byte. The last byte would be ‘10101000’ as this process is repeated. This would make the original code of ‘01110101 00101000' turns to ‘11100111 10010100 10101000’ with the different colours showing where each set of digits has ended up. It is interesting that, in the case of this Kanji character, using UTF-8 makes it take up more space than before; so, in the case of this character, it would be more efficient to use UTF-16 as it does not have the added digits at the start of every byte that UTF-8 requires. This is unusual as it is usually UTF-8 that is credited with using less space.

Interactives below from:
http://csfieldguide.org.nz/en/chapters/data-representation.html

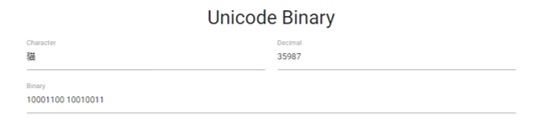
Another good example of this is in the following images. The image directly below is the UTF-8 code for the character 貓. As we can see, 3 bytes are required to accommodate for it.










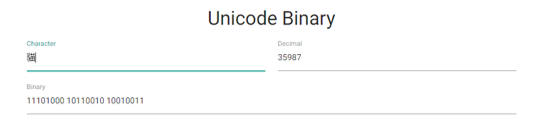
The following image however, shows the same character written in UTF-16 which takes up less space than the variant in UTF-8 as it only uses 2 bytes to represent the character.